Page 253 - 881414_FIZYKA_podrecznik_kl_8_PP_fiipbook

Powtórzenie materiału z klas 7–8

Wielkości fizyczne, jednostki, wzory i ich zastosowanie

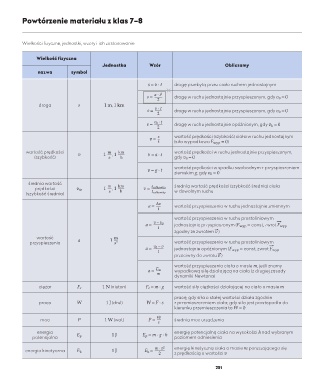
Wielkość fizyczna
Jednostka Wzór Obliczamy
nazwa symbol
s = v · t drogę przebytą przez ciało ruchem jednostajnym

s = a · t 2 drogę w ruchu jednostajnie przyspieszonym, gdy v 0 = 0
2
droga s 1 m, 1 km
s = v · t drogę w ruchu jednostajnie przyspieszonym, gdy v 0 = 0
2
v 0 · t
s = drogę w ruchu jednostajnie opóźnionym, gdy v k = 0
2
v = s wartość prędkości (szybkość) ciała w ruchu jednostajnym
t (siła wypadkowa F wyp = 0)
wartość prędkości v 1 m , 1 km v = a · t wartość prędkości w ruchu jednostajnie przyspieszonym,
(szybkość) s h gdy v 0 = 0

v = g · t wartość prędkości w spadku swobodnym z przyspieszeniem
ziemskim g, gdy v 0 = 0
średnia wartość m km średnią wartość prędkości (szybkość średnią) ciała
prędkości v śr 1 , 1 v = s całkowita
(szybkość średnia) s h t całkowity w dowolnym ruchu

∆v
a = wartość przyspieszenia w ruchu jednostajnie zmiennym
t
wartość przyspieszenia w ruchu prostoliniowym
a = v – v 0 jednostajnie przyspieszonym (F wyp = const, zwrot F wyp
t
zgodny ze zwrotem v )
wartość m
przyspieszenia a 1 s 2 wartość przyspieszenia w ruchu prostoliniowym
a = v 0 – v jednostajnie opóźnionym (F wyp = const, zwrot F wyp
t
przeciwny do zwrotu v )
wartość przyspieszenia ciała o masie m, jeśli znamy
a = F w wypadkową siłę działającą na ciało (z drugiej zasady
m
dynamiki Newtona)
ciężar F c 1 N (niuton) F c = m · g wartość siły ciężkości działającej na ciało o masie m
pracę, gdy siła o stałej wartości działa zgodnie
praca W 1 J (dżul) W = F · s z przemieszczeniem ciała; gdy siła jest prostopadła do
kierunku przemieszczenia to W = 0

moc P 1 W (wat) P = W średnią moc urządzenia
t
energia energię potencjalną ciała na wysokości h nad wybranym
potencjalna E p 1 J E p = m · g · h poziomem odniesienia

energia kinetyczna E k 1 J E k = m · v 2 energię kinetyczną ciała o masie m poruszającego się
z prędkością o wartości v
2
251