Page 24 - 881414_FIZYKA_podrecznik_kl_8_PP_fiipbook
P. 24
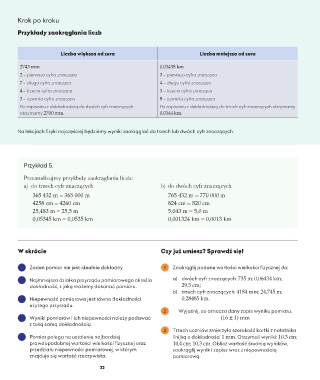
Krok po kroku
Przykłady zaokrąglania liczb
Liczba większa od zera Liczba mniejsza od zera
2743 mm 0,03438 km
2 – pierwsza cyfra znacząca 3 – pierwsza cyfra znacząca
7 – druga cyfra znacząca 4 – druga cyfra znacząca
4 – trzecia cyfra znacząca 3 – trzecia cyfra znacząca
3 – czwarta cyfra znacząca 8 – czwarta cyfra znacząca
Po zapisaniu z dokładnością do dwóch cyfr znaczących Po zapisaniu z dokładnością do trzech cyfr znaczących otrzymamy
otrzymamy 2700 mm. 0,0344 km.
Na lekcjach fizyki najczęściej będziemy wyniki zaokrąglać do trzech lub dwóch cyfr znaczących.
Przykład 5.
Przeanalizujmy przykłady zaokrąglania liczb:
a) do trzech cyfr znaczących b) do dwóch cyfr znaczących
365 432 m = 365 000 m 765 432 m = 770 000 m
4258 cm = 4260 cm 824 cm = 820 cm
25,483 m = 25,5 m 5,043 m = 5,0 m
0,05345 km = 0,0535 km 0,001324 km = 0,0013 km
W skrócie Czy już umiesz? Sprawdź się!
Żaden pomiar nie jest idealnie dokładny. 1 Zaokrąglij podane wartości wielkości fizycznej do:
Najmniejsza działka przyrządu pomiarowego określa a) dwóch cyfr znaczących: 735 m; 0,06434 km;
dokładność, z jaką możemy dokonać pomiaru. 29,5 cm;
b) trzech cyfr znaczących: 4184 mm; 24,745 m;
Niepewność pomiarowa jest równa dokładności 0,28485 km.
użytego przyrządu.
2 Wyjaśnij, co oznacza dany zapis wyniku pomiaru.
Wyniki pomiarów i ich niepewności należy podawać (16 ± 1) mm
z taką samą dokładnością.
3 Trzech uczniów zmierzyło szerokość kartki z notatnika
Pomiar polega na ustaleniu najbardziej linijką o dokładności 1 mm. Otrzymali wyniki: 10,3 cm;
prawdopodobnej wartości wielkości fizycznej oraz 10,4 cm; 10,3 cm. Oblicz wartość średnią wyników,
przedziału niepewności pomiarowej, w którym zaokrąglij wynik i zapisz wraz z niepewnością
znajduje się wartość rzeczywista. pomiarową.
22