Page 138 - kl 7 cz 2

3 W równoległoboku ABCD, w którym AB||CD, na bokach AB i CD
obrano takie punkty K i L, że |AK| = |CL|. Uzasadnij, że czworokąty
AKLD i KLCB mają równe pola.

4 W równoległoboku ABCD, w którym AB||CD, na boku AB obrano
punkt E, na boku BC – punkt F, na boku CD – punkt G, a na boku
DA – punkt H w taki sposób, że odcinek FH jest równoległy do boku
AB. Uzasadnij, że pole czworokąta EFGH jest równe połowie pola
równoległoboku ABCD.

ef
Przekątne deltoidu przecinają się pod 5 Uzasadnij, że pole deltoidu o przekątnych e i f jest równe P = .
2
kątem prostym.
6 Przekątne AC i BD deltoidu ABCD przecinają się w punkcie S, przy
a b czym |AS| = 3|SC|. Uzasadnij, że pole trójkąta ABD jest trzy razy
f większe od pola trójkąta ACD.
e
7 W sześciokącie foremnym ABCDEF, w którym AB||DE, na boku AB
a b zaznaczono punkt G. Uzasadnij, że pole sześciokąta ABCDEF jest trzy
razy większe od pola trójkąta EDG.

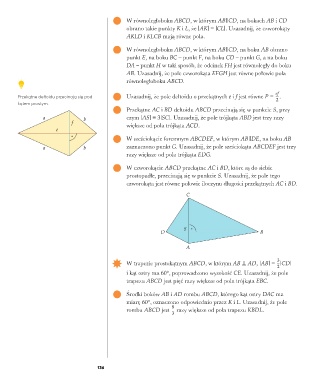
8 W czworokącie ABCD przekątne AC i BD, które są do siebie
prostopadłe, przecinają się w punkcie S. Uzasadnij, że pole tego
czworokąta jest równe połowie iloczynu długości przekątnych AC i BD.
C

S
D B

A

3
9 W trapezie prostokątnym ABCD, w którym AB  AD, |AB| = |CD|
2
i kąt ostry ma 60°, poprowadzono wysokość CE. Uzasadnij, że pole
trapezu ABCD jest pięć razy większe od pola trójkąta EBC.

10 Środki boków AB i AD rombu ABCD, którego kąt ostry DAC ma
miarę 60°, oznaczono odpowiednio przez K i L. Uzasadnij, że pole
8
rombu ABCD jest razy większe od pola trapezu KBDL.
3

136