Page 134 - kl 7 cz 2
P. 134
Zadania
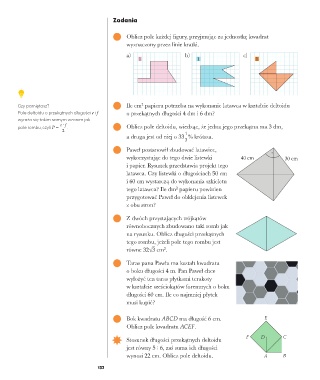
1 Oblicz pole każdej figury, przyjmując za jednostkę kwadrat
wyznaczony przez linie kratki.
a) b) c)
1 1 1
2
Czy pamiętasz? 2 Ile cm papieru potrzeba na wykonanie latawca w kształcie deltoidu
Pole deltoidu o przekątnych długości e i f o przekątnych długości 4 dm i 6 dm?
wyraża się takim samym wzorem jak
e · f
pole rombu, czyli P = . 3 Oblicz pole deltoidu, wiedząc, że jedna jego przekątna ma 3 dm,
2 1
a druga jest od niej o 33 % krótsza.
3
4 Paweł postanowił zbudować latawiec,
wykorzystując do tego dwie listewki 40 cm 30 cm
i papier. Rysunek przedstawia projekt tego
latawca. Czy listewki o długościach 50 cm
i 60 cm wystarczą do wykonania szkieletu
tego latawca? Ile dm papieru powinien
2
przygotować Paweł do obklejenia listewek
z obu stron?
5 Z dwóch przystających trójkątów
równobocznych zbudowano taki romb jak
na rysunku. Oblicz długości przekątnych
tego rombu, jeżeli pole tego rombu jest
2
równe 32 3 cm .
6 Taras pana Pawła ma kształt kwadratu
o boku długości 4 m. Pan Paweł chce
wyłożyć ten taras płytkami terakoty
w kształcie sześciokątów foremnych o boku
długości 60 cm. Ile co najmniej płytek
musi kupić?
7 Bok kwadratu ABCD ma długość 6 cm. E
Oblicz pole kwadratu ACEF.
8 Stosunek długości przekątnych deltoidu F D C
jest równy 5 : 6, zaś suma ich długości
wynosi 22 cm. Oblicz pole deltoidu. A B
132