Page 35 - kl 6 cz 1

Pokażemy teraz inny sposób rozumowania, jaki można zastosować, aby dodać liczby całkowite.

Przykład 1

Na I etapie konkursu matematycznego uczestnikom zadano po 20 pytań. Za poprawną
odpowiedź każdy z nich otrzymywał punkt dodatni (1), za niepoprawną punkt ujemny (–1),
a za brak odpowiedzi uczestnik nie otrzymywał żadnego punktu. Tabela pokazuje liczbę
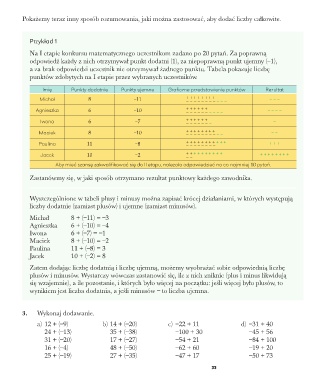
punktów zdobytych na I etapie przez wybranych uczestników.

Imię Punkty dodatnie Punkty ujemne Graficzne przedstawienie punktów Rezultat

Michał 8 –11 + + + + + + + + – – –
– – – – – – – – – – –
Agnieszka 6 –10 + + + + + + – – – –
– – – – – – – – – –
Iwona 6 –7 + + + + + + –
– – – – – – –
Maciek 8 –10 + + + + + + + + – –
– – – – – – – – – –
Paulina 11 –8 + + + + + + + + + + + + + +
– – – – – – – –
Jacek 10 –2 + + + + + + + + + + + + + + + + + +
– –
Aby mieć szansę zakwalifikować się do II etapu, należało odpowiedzieć na co najmniej 10 pytań.

Zastanówmy się, w jaki sposób otrzymano rezultat punktowy każdego zawodnika.

Wyszczególnione w tabeli plusy i minusy można zapisać krócej działaniami, w których występują
liczby dodatnie (zamiast plusów) i ujemne (zamiast minusów).

Michał 8 + (–11) = –3
Agnieszka 6 + (–10) = –4
Iwona 6 + (–7) = –1
Maciek 8 + (–10) = –2
Paulina 11 + (–8) = 3
Jacek 10 + (–2) = 8

Zatem dodając liczbę dodatnią i liczbę ujemną, możemy wyobrażać sobie odpowiednią liczbę
plusów i minusów. Wystarczy wówczas zastanowić się, ile z nich zniknie (plus i minus likwidują
się wzajemnie), a ile pozostanie, i których było więcej na początku: jeśli więcej było plusów, to
wynikiem jest liczba dodatnia, a jeśli minusów – to liczba ujemna.

3. Wykonaj dodawanie.
a) 12 + (–9) b ) 14 + (–20) c ) –22 + 11 d) –31 + 40
24 + (–13) 35 + (–38) –100 + 30 –45 + 56
31 + (–20) 17 + (–27) –54 + 21 –84 + 100
16 + (–4) 48 + (–50) –62 + 60 –19 + 20
25 + (–19) 27 + (–35) –47 + 17 –50 + 73

33