Page 37 - kl 6 cz 1

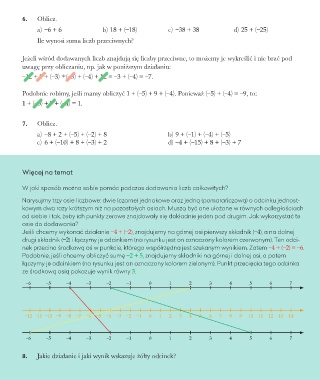
6. Oblicz.
a) –6 + 6 b ) 18 + (–18) c ) –38 + 38 d ) 25 + (–25)

Ile wynosi suma liczb przeciwnych?

Jeżeli wśród dodawanych liczb znajdują się liczby przeciwne, to możemy je wykreślić i nie brać pod
uwagę przy obliczaniu, np. jak w poniższym działaniu:
–12 + 8 + (–3) +(–8) + (–4) + 12 = –3 + (–4) = –7.

Podobnie robimy, jeśli mamy obliczyć 1 + (–5) + 9 + (–4). Ponieważ (–5) + (–4) = –9, to:

1 + (–5) + 9 + (–4) = 1.

7. Oblicz.

a) –8 + 2 + (–5) + (–2) + 8 b) 9 + (–1) + (–4) + (–5)
c) 6 + (–10) + 8 + (–3) + 2 d) –4 + (–15) + 8 + (–3) + 7

Więcej na temat

W jaki sposób można sobie pomóc podczas dodawania liczb całkowitych?

Narysujmy trzy osie liczbowe: dwie (czarne) jednakowe oraz jedną (pomarańczową) o odcinku jednost-
kowym dwa razy krótszym niż na pozostałych osiach. Muszą być one ułożone w równych odległościach
od siebie i tak, żeby ich punkty zerowe znajdowały się dokładnie jeden pod drugim. Jak wykorzystać te
osie do dodawania?
Jeśli chcemy wykonać działanie –4 + (–2), znajdujemy na górnej osi pierwszy składnik (–4), a na dolnej
drugi składnik (–2) i łączymy je odcinkiem (na rysunku jest on oznaczony kolorem czerwonym). Ten odci-
nek przecina środkową oś w punkcie, którego współrzędna jest szukanym wynikiem. Zatem –4 + (–2) = –6.
Podobnie, jeśli chcemy obliczyć sumę –2 + 5, znajdujemy składniki na górnej i dolnej osi, a potem
łączymy je odcinkiem (na rysunku jest on oznaczony kolorem zielonym). Punkt przecięcia tego odcinka
ze środkową osią pokazuje wynik równy 3.
–6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7

–12 –11 –10 –9 –8 –7 –6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

–6 –5 –4 –3 –2 –1 0 1 2 3 4 5 6 7

8. Jakie działanie i jaki wynik wskazuje żółty odcinek?

35