Page 14 - kl 7 cz 2

5.2 Wzajemne położenie prostych na płaszczyźnie

Podejmij temat s t n
p m

r
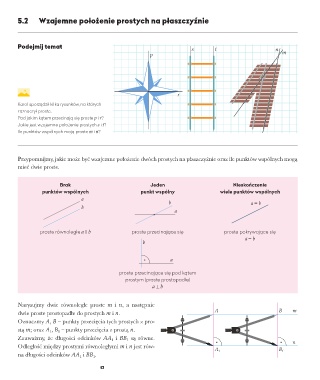
Karol sporządził kilka rysunków, na których
zaznaczył proste.
Pod jakim kątem przecinają się proste p i r?
Jakie jest wzajemne położenie prostych s i t?
Ile punktów wspólnych mają proste m i n?

Przypomnijmy, jakie może być wzajemne położenie dwóch prostych na płaszczyźnie oraz ile punktów wspólnych mogą
mieć dwie proste.

Brak Jeden Nieskończenie
punktów wspólnych punkt wspólny wiele punktów wspólnych
a b a = b
b
a

proste równoległe a || b proste przecinające się proste pokrywające się
a = b
b

a

proste przecinające się pod kątem
prostym (proste prostopadłe)
a  b

Narysujmy dwie równoległe proste m i n, a następnie
dwie proste prostopadłe do prostych m i n. A B m

Oznaczmy A, B – punkty przecięcia tych prostych z pro-
stą m; oraz A , B – punkty przecięcia z prostą n.
1
1
Zauważmy, że długości odcinków AA i BB są równe.
1
1
Odległość między prostymi równoległymi m i n jest rów- n
A 1 B 1
na długości odcinków AA i BB .
1
1
12