Page 16 - kl 7 cz 2

Przykład 1 k

b 4 b 3 b
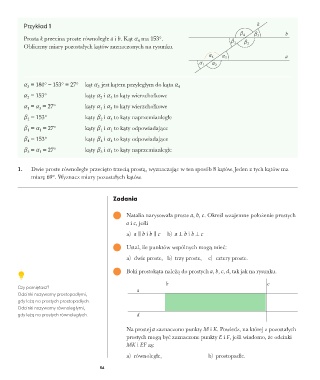
Prosta k przecina proste równoległe a i b. Kąt a ma 153°. b 1
4
Obliczmy miary pozostałych kątów zaznaczonych na rysunku. b 2
a 4 a 3 a
a 1 a 2

a = 180° – 153° = 27° kąt a jest kątem przyległym do kąta a 4
3
3
a = 153° kąty a i a to kąty wierzchołkowe
2
2
4
a = a = 27° kąty a i a to kąty wierzchołkowe
1
3
3
1
b = 153° kąty b i a to kąty naprzemianległe
4
2
2
b = a = 27° kąty b i a to kąty odpowiadające
1
1
1
1
b = 153° kąty b i a to kąty odpowiadające
4
4
4
b = a = 27° kąty b i a to kąty naprzemianległe
1
3
3
1
1. Dwie proste równoległe przecięto trzecią prostą, wyznaczając w ten sposób 8 kątów. Jeden z tych kątów ma
miarę 69°. Wyznacz miary pozostałych kątów.
Zadania
1 Natalia narysowała proste a, b, c. Określ wzajemne położenie prostych
a i c, jeśli
a) a || b i b || c b) a  b i b  c

2 Ustal, ile punktów wspólnych mogą mieć:
a) dwie proste, b) trzy proste, c) cztery proste.

3 Boki prostokąta należą do prostych a, b, c, d, tak jak na rysunku.
b c
Czy pamiętasz? a
Odcinki nazywamy prostopadłymi,
gdy leżą na prostych prostopadłych.
Odcinki nazywamy równoległymi,
gdy leżą na prostych równoległych. d

Na prostej a zaznaczono punkty M i K. Powiedz, na której z pozostałych
prostych mogą być zaznaczone punkty E i F, jeśli wiadomo, że odcinki
MK i EF są:

a) równoległe, b) prostopadłe.

14