Page 153 - 881414_FIZYKA_podrecznik_kl_8_PP_fiipbook

Wartość prędkości (szybkość) w ruchu prostoliniowym jednostajnie
przyspieszonym bez szybkości początkowej jest równa iloczynowi wartości
przyspieszenia i czasu trwania ruchu.
v = a · t

m
s
Jeśli szybkość początkowa jest różna od zera (v 0 ≠ 0), to po przekształce- v ( )
niu wzoru a = v – v 0 otrzymujemy v = v 0 + a · t. 0,8
t
m
Wykorzystujemy ponownie wyniki doświadczenia z kulką (a = 0,2 ), ob- 0,6
s
2
liczamy wartości prędkości po pierwszej, drugiej, trzeciej, czwartej sekundzie, 0,4
korzystając ze wzoru: v = a · t 0,2
m
• v 1 = a · t 1 = 0,2 · 1 s = 0,2 m Na podstawie tych danych spo-
s
s
2
m
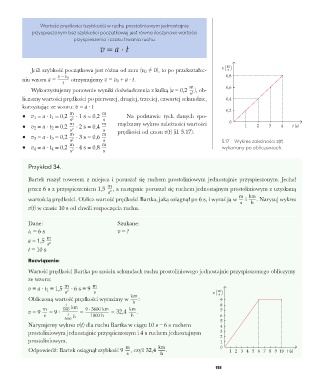
• v 2 = a · t 2 = 0,2 · 2 s = 0,4 m rządzamy wykres zależności wartości 0 1 2 3 4 t (s)
s
s
2
prędkości od czasu v(t) (il. 5.17).
m
• v 3 = a · t 3 = 0,2 · 3 s = 0,6 m
s
s
2
m m 5.17 Wykres zależności v(t)
• v 4 = a · t 4 = 0,2 · 4 s = 0,8 s wykonany po obliczeniach.
s
2
Przykład 34.
Bartek ruszył rowerem z miejsca i poruszał się ruchem prostoliniowym jednostajnie przyspieszonym. Jechał
m
przez 6 s z przyspieszeniem 1,5 , a następnie poruszał się ruchem jednostajnym prostoliniowym z uzyskaną
s
2
m
wartością prędkości. Oblicz wartość prędkości Bartka, jaką osiągnął po 6 s, i wyraź ją w i km . Narysuj wykres
h
s
v(t) w czasie 10 s od chwili rozpoczęcia ruchu.
Dane: Szukane:
t 1 = 6 s v = ?
a = 1,5 m 2
s
t = 10 s
Rozwiązanie:
Wartość prędkości Bartka po sześciu sekundach ruchu prostoliniowego jednostajnie przyspieszonego obliczymy
ze wzoru:
m
v = a · t 1 = 1,5 · 6 s = 9 m v ( )
m
s
s
2
s
Obliczoną wartość prędkości wyrazimy w km : 9
1 km h 8
m
v = 9 = 9 · 1000 = 9 · 3600 km = 32,4 km . 7
s 1 h 1000 h h 6
3600 5
Narysujemy wykres v(t) dla ruchu Bartka w ciągu 10 s – 6 s ruchem 4
prostoliniowym jednostajnie przyspieszonym i 4 s ruchem jednostajnym 3 2
prostoliniowym. 1
m
Odpowiedź: Bartek osiągnął szybkość 9 , czyli 32,4 km . 0 1 2 3 4 5 6 7 8 9 10 t (s)
s
h
151