Page 124 - kl 7 cz 2

T
8.5
8.5 Trapezyrapezy

P
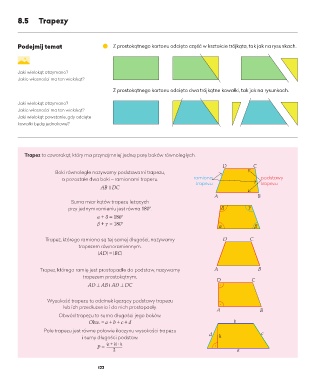
Podejmij tematodejmij temat Z prostokątnego kartonu odcięto część w kształcie trójkąta, tak jak na rysunkach.

Jaki wielokąt otrzymano?
Jakie własności ma ten wielokąt?

Z prostokątnego kartonu odcięto dwa trójkątne kawałki, tak jak na rysunkach.

Jaki wielokąt otrzymano?
Jakie własności ma ten wielokąt?
Jaki wielokąt powstanie, gdy odcięte
kawałki będą jednakowe?

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych.
D C
Boki równoległe nazywamy podstawami trapezu,
a pozostałe dwa boki – ramionami trapezu. ramiona podstawy
trapezu
trapezu
AB || DC
A B
Suma miar kątów trapezu leżących
przy jednym ramieniu jest równa 180°. d c
a + d = 180°
b + c = 180°
a b

Trapez, którego ramiona są tej samej długości, nazywamy D C
trapezem równoramiennym.
|AD| = |BC|

Trapez, którego ramię jest prostopadłe do podstaw, nazywamy A B
trapezem prostokątnym. D C
AD  AB i AD  DC

Wysokość trapezu to odcinek łączący podstawy trapezu
lub ich przedłużenia i do nich prostopadły.
A B
Obwód trapezu to suma długości jego boków.
Obw. = a + b + c + d b
Pole trapezu jest równe połowie iloczynu wysokości trapezu c
i sumy długości podstaw. d h
(a + b) · h
P = 2 a

122