Page 150 - kl 7 cz 2

9.2 Długości odcinków w układzie współrzędnych

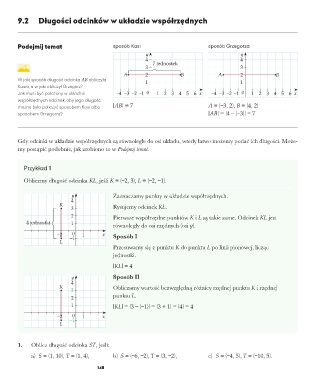
Podejmij temat sposób Kasi sposób Grzegorza
4 7 jednostek 4
3 3
A 2 B A 2 B
W jaki sposób długość odcinka AB obliczyła 1 1
Kasia, a w jaki obliczył Grzegorz?
Jak musi być położony w układzie –4 –3 –2 –1 0 1 2 3 4 5 6 x –4 –3 –2 –1 0 1 2 3 4 5 6 x
współrzędnych odcinek, aby jego długość
można było policzyć sposobem Kasi albo |AB| = 7 A = (–3, 2), B = (4, 2)
sposobem Grzegorza? |AB| = |4 – (–3)| = 7

Gdy odcinki w układzie współrzędnych są równoległe do osi układu, wtedy łatwo możemy podać ich dlugości. Może-
my postąpić podobnie, jak zrobiono to w Podejmij temat.

Przykład 1

Obliczmy długość odcinka KL, jeśli K = (–2, 3), L = (–2, –1).

4 Zaznaczamy punkty w układzie współrzędnych.
K 3 Rysujemy odcinek KL.

2 Pierwsze współrzędne punktów K i L są takie same. Odcinek KL jest
4 jednostki 1 równoległy do osi rzędnych (osi y).

0
–2 –1 1 x Sposób I

L
Przesuwamy się z punktu K do punktu L po linii pionowej, licząc
jednostki.
|KL| = 4

Sposób II
4
K 3 Obliczamy wartość bezwzględną różnicy rzędnej punktu K i rzędnej
2 punktu L.
1 |KL| = |3 – (–1)| = |3 + 1| = |4| = 4
0
–2 –1 1 x
L

1. Oblicz długość odcinka ST, jeśli:

a) S = (1, 10), T = (1, 4), b) S = (–6, –2), T = (3, –2), c) S = (–4, 5), T = (–10, 5).

148