Page 151 - kl 7 cz 2

Więcej na temat

Odcinek, którego końce nie znajdują się w punktach kratowych, trudno jest narysować w układzie współrzędnych.
Jeżeli jednak ten odcinek jest równoległy do jednej z osi (czyli rzędne albo odcięte końców odcinka są takie same),
to długość tego odcinka możemy obliczyć, korzystając z II sposobu z przykładu 1.
Obliczmy długość odcinka AB, jeśli A = (2 3, 4 3 ), B = (–10 3, 4 3 ). Rzędne punktów są takie same.

|AB| = |2 3 – (–10 3 )| = |2 3 + 10 3| = 12 3

2. Oblicz długość odcinka CD, jeśli:
3
3
3
3
a) C = ( 4, –7 6 ), D = ( 4, 3 6 ), b) C = (13 7, –1 ), D = (5 7, –1 ), c) C = (–2 5, 3 ), D = (–7 5, 3 ).
Gdy odcinek w układzie współrzędnych nie jest równoległy do osi układu,
wtedy możemy obliczyć jego długość, korzystając z twierdzenia Pitagorasa.

Przykład 2

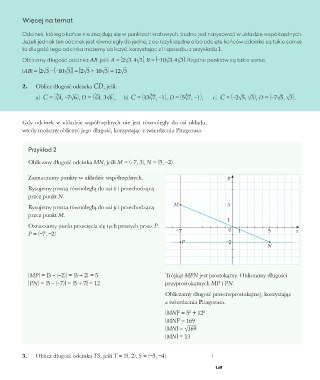
Obliczmy długość odcinka MN, jeśli M = (–7, 3), N = (5, –2).

Zaznaczamy punkty w układzie współrzędnych.

Rysujemy prostą równoległą do osi x i przechodzącą
przez punkt N.
Rysujemy prostą równoległą do osi y i przechodzącą M 3
przez punkt M.
1
Oznaczamy punkt przecięcia się tych prostych przez P. 0
P = (–7, –2) –7 1 5 x
P –2
N

|MP| = |3 – (–2)| = |3 + 2| = 5 Trójkąt MPN jest prostokątny. Obliczamy długości
|PN| = |5 – (–7)| = |5 + 7| = 12 przyprostokątnych MP i PN.

Obliczamy długość przeciwprostokątnej, korzystając
z twierdzenia Pitagorasa.

2
2
|MN| = 5 + 12 2
|MN| = 169
2
|MN| = 169
|MN| = 13

3. Oblicz długość odcinka TS, jeśli T = (5, 2), S = (–3, –4).

149