Page 155 - kl 7 cz 2

6. Narysuj w układzie współrzędnych odcinek EF, jeśli E = (1, 4),
F = (8, 3). Narysuj odcinek RS prostopadły do odcinka EF, o tej samej
długości, co odcinek EF. Sprawdź za pomocą ekierki poprawność
wykonanego ćwiczenia.

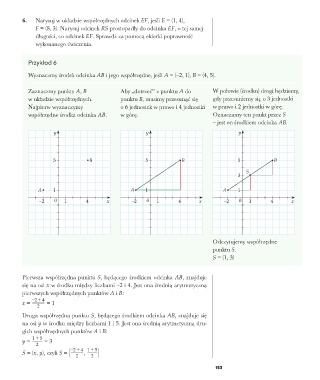
Przykład 6

Wyznaczmy środek odcinka AB i jego współrzędne, jeśli A = (–2, 1), B = (4, 5).

Zaznaczmy punkty A, B Aby „dotrzeć” z punktu A do W połowie (środku) drogi będziemy,
w układzie współrzędnych. punktu B, musimy przesunąć się gdy przesuniemy się o 3 jednostki
Najpierw wyznaczymy o 6 jednostek w prawo i 4 jednostki w prawo i 2 jednostki w górę.
współrzędne środka odcinka AB. w górę. Oznaczamy ten punkt przez S
– jest on środkiem odcinka AB.

5 B 5 B 5 B

S
3

A 1 A 1 A 1

–2 0 1 4 x –2 0 1 4 x –2 0 1 4 x

Odczytujemy współrzędne
punktu S.
S = (1, 3)

Pierwsza współrzędna punktu S, będącego środkiem odcinka AB, znajduje
się na osi x w środku między liczbami –2 i 4. Jest ona średnią arytmetyczną
pierwszych współrzędnych punktów A i B:
x = –2 + 4 = 1
2
Druga współrzędna punktu S, będącego środkiem odcinka AB, znajduje się
na osi y w środku między liczbami 1 i 5. Jest ona średnią arytmetyczną dru-
gich współrzędnych punktów A i B:
y = 1 + 5 = 3
2
S = (x, y), czyli S = ( –2 + 4 1 + 5 )
,
2
2
153