Page 156 - kl 7 cz 2

)
)
Aby wyznaczyć współrzędne środka odcinka AB, gdzie A = (x A, y A , B = (x B, y B ,
należy wyznaczyć średnie arytmetyczne odpowiednich współrzędnych
jego końców.
x y
S = ( x A + B , A + B )
y
2
2

7. Wyznacz środek odcinka AB, jeśli A = (–10, 3), B = (–4, –5).

Przykład 7

Punkt S = (1, 1) jest środkiem odcinka AB takiego, że A = (–2, 3).
Obliczymy współrzędne punktu B.

Przyjmijmy, że B = (x , y ).
B
B
Wiemy, że x = x A + x B , y = y A + y B oraz że x = –2, y = 3, x = 1, y = 1
S
S
S
A
A
S
2
2
–2 + x B = 1 3 + y B = 1
2 2
–2 + x = 2 3 + y = 2
B
B
x = 4 y = –1
B
B
B = (4, –1)
8. Punkt S = (0, 3) jest środkiem odcinka AB takiego, że B = (4, –1).
Oblicz współrzędne punktu A.

Zadania

1 Oblicz długość odcinka PR, jeśli:

a) P = (–4, –7), R = (–4, 3), b) P = (–5, 2), R = (–3, 2), c) P = (2, –4), R = (10, 2),
d) P = (0, –6), R = (2, 0), e) P = (–1, –8), R = (7, 7), f) P = (41, 83), R = (34, 59).

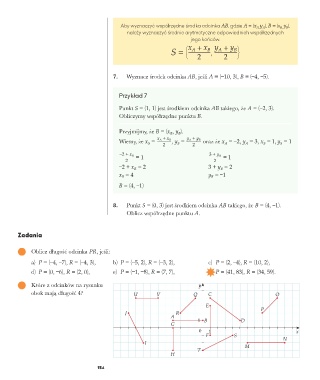
2 Które z odcinków na rysunku
obok mają długość 4? U V Q C O

E
J R P
A
G 1 B D
0 1 x
F S N
I M
T
H

154