Page 160 - kl 7 cz 2

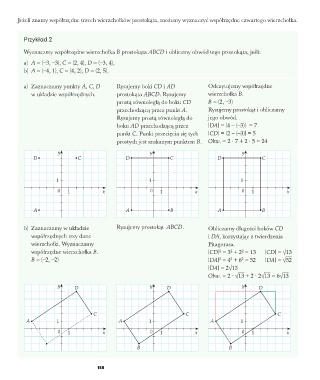
Jeżeli znamy współrzędne trzech wierzchołków prostokąta, możemy wyznaczyć współrzędne czwartego wierzchołka.

Przykład 2

Wyznaczmy współrzędne wierzchołka B prostokąta ABCD i obliczmy obwód tego prostokąta, jeśli:

a) A = (–3, –3), C = (2, 4), D = (–3, 4),
b) A = (–4, 1), C = (4, 2), D = (2, 5).

a) Zaznaczamy punkty A, C, D Rysujemy boki CD i AD Odczytujemy współrzędne
w układzie współrzędnych. prostokąta ABCD. Rysujemy wierzchołka B.
prostą równoległą do boku CD B = (2, –3)
przechodzącą przez punkt A. Rysujemy prostokąt i obliczamy
Rysujemy prostą równoległą do jego obwód.
boku AD przechodzącą przez |DA| = |4 – (–3)| = 7
punkt C. Punkt przecięcia się tych |CD| = |2 – (–3)| = 5
prostych jest szukanym punktem B. Obw. = 2 ∙ 7 + 2 ∙ 5 = 24

D C D C D C

1 1 1
0 1 x 0 1 x 0 1 x

A A B A B

b) Zaznaczamy w układzie Rysujemy prostokąt ABCD. Obliczamy długości boków CD
współrzędnych trzy dane i DA, korzystając z twierdzenia
wierzchołki. Wyznaczamy Pitagorasa.
współrzędne wierzchołka B. |CD| = 3 + 2 = 13 |CD| = 13
2
2
2
B = (–2, –2) |DA| = 4 + 6 = 52 |DA| = 52
2
2
2
|DA| = 2 13
Obw. = 2 ∙ 13 + 2 ∙ 2 13 = 6 13
D D D

C C C
A 1 A 1 A 1

0 1 x 0 1 x 0 1 x

B B

158