Page 165 - kl 7 cz 2

9.4 Pola figur w układzie współrzędnych

Podejmij temat Zasady gry
1. Gracz rzuca trzykrotnie dwiema kostkami.
2. Liczby oczek wyrzuconych na kostkach są współrzędnymi punktu w układzie
współrzędnych, przy czym gracz decyduje, która liczba będzie pierwszą,
a która drugą współrzędną.
3. Jeśli trzykrotnie zostanie wyrzucona ta sama para liczb, ostatni rzut
powtarza się aż do momentu uzyskania innej pary liczb.
4. Zaznaczone trzy punkty są wierzchołkami trójkąta.
5. Wygrywa ten gracz, który narysuje trójkąt o większym polu.
6. Jeśli trzy punkty narysowane są w jednej linii, gracz przegrywa.

Jakie pole ma trójkąt narysowany przez
Magdę?
Karol w ostatnim rzucie na jednej kostce
wyrzucił 2 oczka, a na drugiej 6 oczek. 1 1
Czy ma szansę wygrać z Magdą? 0 1 x 0 1 x
Punkt o jakich współrzędnych powinien
zaznaczyć Karol, aby wygrać z Magdą? wynik Magdy wynik Karola

Jeśli potrafimy obliczyć długości odcinków w układzie współrzędnych, możemy
obliczać pola figur w układzie współrzędnych, korzystając ze znanych wzorów.

Przykład 1

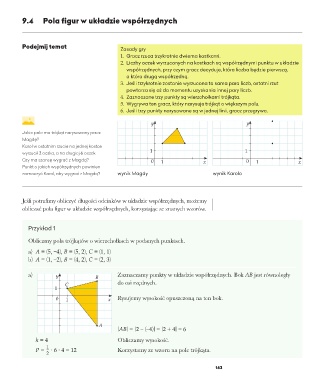
Obliczmy pola trójkątów o wierzchołkach w podanych punktach.

a) A = (5, –4), B = (5, 2), C = (1, 1)
b) A = (1, –2), B = (4, 2), C = (2, 3)

a) B Zaznaczamy punkty w układzie współrzędnych. Bok AB jest równoległy

C do osi rzędnych.
1
0 1 x Rysujemy wysokość opuszczoną na ten bok.

A
|AB| = |2 – (–4)| = |2 + 4| = 6

h = 4 Obliczamy wysokość.
1
P = · 6 · 4 = 12 Korzystamy ze wzoru na pole trójkąta.
2

163