Page 23 - kl 7 cz 2

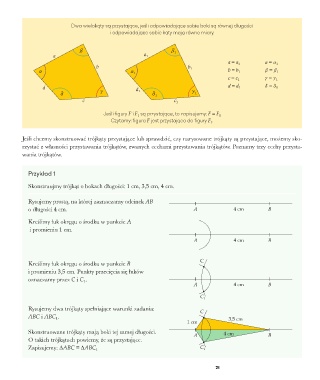
Dwa wielokąty są przystające, jeśli odpowiadające sobie boki są równej długości
i odpowiadające sobie kąty mają równe miary.

b b 1
a a 1

a = a 1 a = a 1
b b 1
a a 1 b = b 1 b = b 1
c = c 1 c = c 1
d d 1 d = d 1 d = d 1
d c d 1 c 1
c c 1

Jeśli figury F i F 1 są przystające, to zapisujemy: F ≡ F 1
Czytamy: figura F jest przystająca do figury F 1 .

Jeśli chcemy skonstruować trójkąty przystające lub sprawdzić, czy narysowane trójkąty są przystające, możemy sko-
rzystać z własności przystawania trójkątów, zwanych cechami przystawania trójkątów. Poznamy trzy cechy przysta-
wania trójkątów.

Przykład 1

Skonstruujmy trójkąt o bokach długości: 1 cm, 3,5 cm, 4 cm.

Rysujemy prostą, na której zaznaczamy odcinek AB
o długości 4 cm. A 4 cm B

Kreślimy łuk okręgu o środku w punkcie A
i promieniu 1 cm.
A 4 cm B

Kreślimy łuk okręgu o środku w punkcie B C
i promieniu 3,5 cm. Punkty przecięcia się łuków
oznaczamy przez C i C .
1
A 4 cm B
C 1
Rysujemy dwa trójkąty spełniające warunki zadania: C
ABC i ABC . 3,5 cm
1
1 cm
Skonstruowane trójkąty mają boki tej samej długości. A 4 cm B
O takich trójkątach powiemy, że są przystające.
Zapisujemy: ∆ABC ≡ ∆ABC 1 C 1

21