Page 112 - kl 8 cz 2

y
2
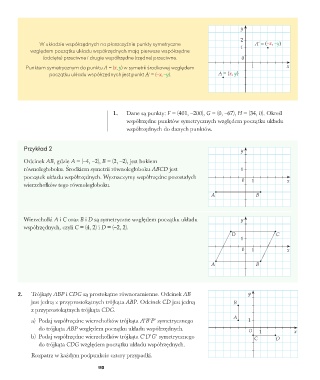
W układzie współrzędnych na płaszczyźnie punkty symetryczne 1 A’ = (–x, –y)
względem początku układu współrzędnych mają pierwsze współrzędne
(odcięte) przeciwne i drugie współrzędne (rzędne) przeciwne. 0
Punktem symetrycznym do punktu A = (x, y) w symetrii środkowej względem 1 x
początku układu współrzędnych jest punkt A’ = (–x, –y). A = (x, y)

1. Dane są punkty: F = (401, –200), G = (0, –67), H = (34, 0). Określ
współrzędne punktów symetrycznych względem początku układu
współrzędnych do danych punktów.

Przykład 2 y

Odcinek AB, gdzie A = (–4, –2), B = (2, –2), jest bokiem
równoległoboku. Środkiem symetrii równoległoboku ABCD jest 1
początek układu współrzędnych. Wyznaczymy współrzędne pozostałych 0 1 x
wierzchołków tego równoległoboku.

A B

Wierzchołki A i C oraz B i D są symetryczne względem początku układu y
współrzędnych, czyli C = (4, 2) i D = (–2, 2).
D C
1
0 1 x

A B

2. Trójkąty ABP i CDG są prostokątne równoramienne. Odcinek AB y
jest jedną z przyprostokątnych trójkąta ABP. Odcinek CD jest jedną B
z przyprostokątnych trójkąta CDG.
A
a) Podaj współrzędne wierzchołków trójkąta A’B’P’ symetrycznego 1
do trójkąta ABP względem początku układu współrzędnych. 0 1 x
b) Podaj współrzędne wierzchołków trójkąta C’D’G’ symetrycznego C D
do trójkąta CDG względem początku układu współrzędnych.

Rozpatrz w każdym podpunkcie cztery przypadki.

110