Page 123 - kl 8 cz 2

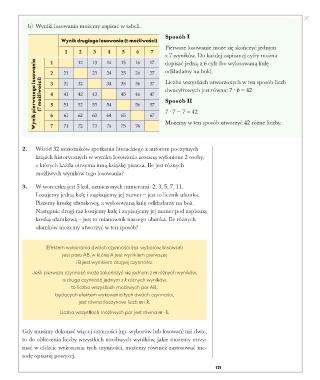
b) Wyniki losowania możemy zapisać w tabeli.

Sposób I
Wynik drugiego losowania (6 możliwości)
Pierwsze losowanie może się skończyć jednym
1 2 3 4 5 6 7
z 7 wyników. Do każdej zapisanej cyfry można
Wynik pierwszego losowania (7 możliwości) 3 31 32 43 34 35 36 37 Liczba wszystkich utworzonych w ten sposób liczb
1
16
15
14
13
dopisać jedną z 6 cyfr (bo wylosowaną kulę
12
17
odkładamy na bok).
2
23
24
21
27
25
26
dwucyfrowych jest równa: 7 · 6 = 42
41
46
47
42
45
4
Sposób II
52
57
5
56
54
53
51
7 · 7 − 7 = 42
63
61
67
65
64
6
62
Możemy w ten sposób utworzyć 42 różne liczby.
7
74
75
76
73
71
72
2. Wśród 32 uczestników spotkania literackiego z autorem poczytnych
książek historycznych w wyniku losowania zostaną wyłonione 2 osoby,
z których każda otrzyma inną książkę pisarza. Ile jest różnych
możliwych wyników tego losowania?
3. W woreczku jest 5 kul, oznaczonych numerami: 2, 3, 5, 7, 11.
Losujemy jedną kulę i zapisujemy jej numer – jest to licznik ułamka.
Piszemy kreskę ułamkową, a wylosowaną kulę odkładamy na bok.
Następnie drugi raz losujemy kulę i zapisujemy jej numer pod zapisaną
kreską ułamkową – jest to mianownik naszego ułamka. Ile różnych
ułamków możemy utworzyć w ten sposób?
Efektem wykonania dwóch czynności (np. wyborów, losowań)
jest para AB, w której A jest wynikiem pierwszej
i B jest wynikiem drugiej czynności.
Jeśli pierwsza czynność może zakończyć się jednym z m różnych wyników,
a druga czynność jednym z k różnych wyników,
to liczba wszystkich możliwych par AB,
będących efektem wykonania tych dwóch czynności,
jest równa iloczynowi liczb m i k.
Liczba wszystkich możliwych par jest równa m · k.
Gdy musimy dokonać więcej czynności (np. wyborów lub losowań) niż dwie,
to do obliczenia liczby wszystkich możliwych wyników, jakie możemy otrzy-
mać w efekcie wykonania tych czynności, możemy również zastosować me-
todę opisaną powyżej.

121