Page 90 - kl 8 cz 2

1. Narysuj dowolny kąt ostry i skonstruuj jego dwusieczną.

Przykład 2

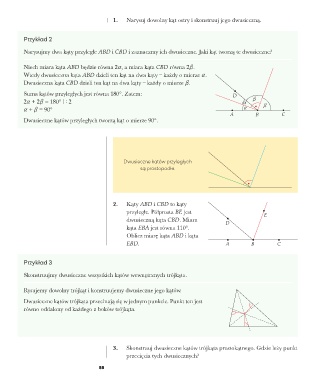
Narysujmy dwa kąty przyległe ABD i CBD i zaznaczmy ich dwusieczne. Jaki kąt tworzą te dwusieczne?

Niech miara kąta ABD będzie równa 2a, a miara kąta CBD równa 2b.
Wtedy dwusieczna kąta ABD dzieli ten kąt na dwa kąty – każdy o mierze a.
Dwusieczna kąta CBD dzieli ten kąt na dwa kąty – każdy o mierze b.
Suma kątów przyległych jest równa 180°. Zatem: D
2a + 2b = 180° | : 2 a b b
a + b = 90° a
A B C
Dwusieczne kątów przyległych tworzą kąt o mierze 90°.

Dwusieczne kątów przyległych
są prostopadłe.

2. Kąty ABD i CBD to kąty
przyległe. Półprosta BE jest E
dwusieczną kąta CBD. Miara D
kąta EBA jest równa 110°.
Oblicz miarę kąta ABD i kąta
EBD. A B C

Przykład 3

Skonstruujmy dwusieczne wszystkich kątów wewnętrznych trójkąta.

Rysujemy dowolny trójkąt i konstruujemy dwusieczne jego kątów.
Dwusieczne kątów trójkąta przecinają się w jednym punkcie. Punkt ten jest
równo oddalony od każdego z boków trójkąta.

3. Skonstruuj dwusieczne kątów trójkąta prostokątnego. Gdzie leży punkt
przecięcia tych dwusiecznych?

88