Page 168 - kl 7 cz 2

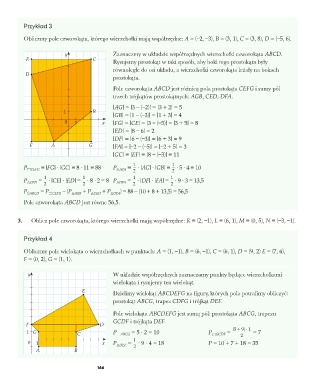
Przykład 3

Obliczmy pole czworokąta, którego wierzchołki mają współrzędne: A = (–2, –3), B = (3, 1), C = (3, 8), D = (–5, 6).

Zaznaczmy w układzie współrzędnych wierzchołki czworokąta ABCD.
E C Rysujemy prostokąt w taki sposób, aby boki tego prostokąta były

równoległe do osi układu, a wierzchołki czworokąta leżały na bokach
D
prostokąta.
Pole czworokąta ABCD jest różnicą pola prostokąta CEFG i sumy pól
trzech trójkątów prostokątnych: AGB, CED, DFA.

1 B |AG| = |3 – (–2)| = |3 + 2| = 5
|GB| = |1 – (–3)| = |1 + 3| = 4
1
0 x |FG| = |CE| = |3 – (–5)| = |3 + 5| = 8
|ED| = |8 – 6| = 2
|DF| = |6 – (–3)| = |6 + 3| = 9
F
A G |FA| = |–2 – (–5)| = |–2 + 5| = 3
|GC| = |EF| = |8 – (–3)| = 11
1
1
P CEFG = |FG| ∙ |GC| = 8 ∙ 11 = 88 P AGB = ∙ |AG| ∙ |GB| = ∙ 5 ∙ 4 = 10
2
2
1
1
1
1
P CED = ∙ |CE| ∙ |ED| = ∙ 8 ∙ 2 = 8 P DFA = ∙ |DF| ∙ |FA| = ∙ 9 ∙ 3 = 13,5
2
2
2
2
P ABCD = P CEFG – (P AGB + P CED + P DFA ) = 88 – (10 + 8 + 13,5) = 56,5
Pole czworokąta ABCD jest równe 56,5.
3. Oblicz pole czworokąta, którego wierzchołki mają współrzędne: K = (2, –1), L = (6, 1), M = (0, 5), N = (–3, –1).
Przykład 4

Obliczmy pole wielokąta o wierzchołkach w punktach: A = (1, –1), B = (6, –1), C = (6, 1), D = (9, 2) E = (7, 6),
F = (0, 2), G = (1, 1).

W układzie współrzędnych zaznaczamy punkty będące wierzchołkami
wielokąta i rysujemy ten wielokąt.

E Dzielimy wielokąt ABCDEFG na figury, których pola potrafimy obliczyć:
prostokąt ABCG, trapez CDFG i trójkąt DEF.

Pole wielokąta ABCDEFG jest sumą pól: prostokąta ABCG, trapezu
GCDF i trójkąta DEF.
F D
1
G P ABCG = 5 ∙ 2 = 10 P GCDF = (5 + 9) · 1 = 7
C
2
1
0 1 x P DEF = ∙ 9 ∙ 4 = 18 P = 10 + 7 + 18 = 35
2
A B
166