Page 107 - kl 8 cz 1

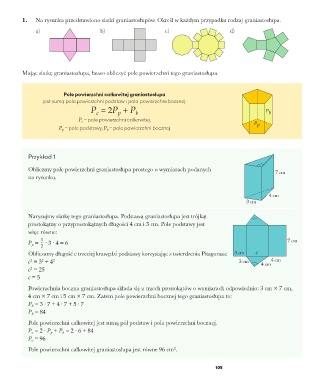
1. Na rysunku przedstawiono siatki graniastosłupów. Określ w każdym przypadku rodzaj graniastosłupa.
a) b) c) d)

Mając siatkę graniastosłupa, łatwo obliczyć pole powierzchni tego graniastosłupa.

Pole powierzchni całkowitej graniastosłupa
jest sumą pola powierzchni podstaw i pola powierzchni bocznej.
P = 2P + P b P b
c
p
P c – pole powierzchni całkowitej, P
P p – pole podstawy, P b – pole powierzchni bocznej p

Przykład 1

Obliczmy pole powierzchni graniastosłupa prostego o wymiarach podanych 7 cm
na rysunku.

4 cm
3 cm

Narysujmy siatkę tego graniastosłupa. Podstawą graniastosłupa jest trójkąt
prostokątny o przyprostokątnych długości 4 cm i 3 cm. Pole podstawy jest
więc równe:
1
P = · 3 · 4 = 6 7 cm
p
2
Obliczamy długość c trzeciej krawędzi podstawy korzystając z twierdzenia Pitagorasa: 3 cm c
c = 3 + 4 2 3 cm 4 cm 4 cm
2
2
c = 25
2
c = 5
Powierzchnia boczna graniastosłupa składa się z trzech prostokątów o wymiarach odpowiednio: 3 cm × 7 cm,
4 cm × 7 cm i 5 cm × 7 cm. Zatem pole powierzchni bocznej tego graniastosłupa to:
P = 3 · 7 + 4 · 7 + 5 · 7
b
P = 84
b
Pole powierzchni całkowitej jest sumą pól podstaw i pola powierzchni bocznej.
P = 2 · P + P = 2 ∙ 6 + 84
c
b
p
P = 96
c
2
Pole powierzchni całkowitej graniastosłupa jest równe 96 cm .
105