Page 24 - kl 8 cz 1

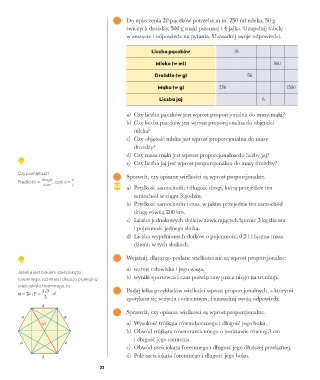
3 Do upieczenia 20 pączków potrzeba m.in. 250 ml mleka, 50 g
świeżych drożdży, 500 g mąki pszennej i 4 jajka. Uzupełnij tabelę
w zeszycie i odpowiedz na pytania. Uzasadnij swoje odpowiedzi.

Liczba pączków 15

Mleko (w ml) 500

Drożdże (w g) 50
Mąka (w g) 250 1500

Liczba jaj 6

a) Czy liczba pączków jest wprost proporcjonalna do masy mąki?
b) Czy liczba pączków jest wprost proporcjonalna do objętości
mleka?
c) Czy objętość mleka jest wprost proporcjonalna do masy
drożdży?
d) Czy masa mąki jest wprost proporcjonalna do liczby jaj?
e) Czy liczba jaj jest wprost proporcjonalna do masy drożdży?
Czy pamiętasz? 4 Sprawdź, czy opisane wielkości są wprost proporcjonalne.
Prędkość = droga , czyli v = s
czas t a) Prędkość samochodu i długość drogi, którą przejedzie ten

samochód w ciągu 3 godzin.
b) Prędkość samochodu i czas, w jakim przejedzie ten samochód

drogę równą 200 km.
c) Liczba jednakowych słoików zawierających łącznie 3 kg dżemu
i pojemność jednego słoika.
d) Liczba wypełnionych słoików o pojemności 0,5 l i łączna masa
dżemu w tych słoikach.

5 Wyjaśnij, dlaczego podane wielkości nie są wprost proporcjonalne:
a) wzrost człowieka i jego waga,
Jeżeli a jest bokiem sześciokąta
foremnego, zaś m jest dłuższą przekątną b) wyniki sportowca i czas poświęcony przez niego na treningi.
sześciokąta foremnego, to:
3 3 6 Podaj kilka przykładów wielkości wprost proporcjonalnych, z którymi
m = 2a i P = · a 2
2 spotykasz się w życiu codziennym, i uzasadnij swoją odpowiedź.
a
7 Sprawdź, czy opisane wielkości są wprost proporcjonalne.
a a
m a) Wysokość trójkąta równobocznego i długość jego boku.
b) Obwód trójkąta równoramiennego o podstawie równej 3 cm
i długość jego ramienia.
a a
c) Obwód sześciokąta foremnego i długość jego dłuższej przekątnej.
a d) Pole sześciokąta foremnego i długość jego boku.

22