Page 135 - kl 8 cz 2

Przykład 2

Na jednej półce Karolina ma dwa swetry białe, jeden zielony, trzy niebieskie i jeden czarny, a na drugiej półce
jedną parę spodni białych, jedną czarnych i dwie pary niebieskich. Karolina chce wyjąć z szafy w sposób
losowy jeden sweter i jedne spodnie. Obliczmy prawdopodobieństwo tego, że:

a) wyjęte z szafy sweter i spodnie będą w tym samym kolorze,
b) wyjęty z szafy sweter będzie w kolorze zielonym lub niebieskim.

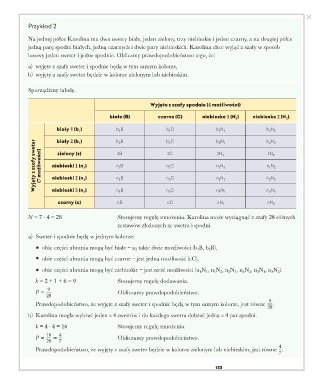
Sporządźmy tabelę.

Wyjęte z szafy spodnie (4 możliwości)

białe (B) czarne (C) niebieske 1 (N 1 ) niebieske 2 (N 2 )

biały 1 (b 1 ) b 1 B b 1 C b 2 N 1 b 2 N 2
b 1 N 1
b 1 N 2
b 2 C
b 2 B
Wyjęty z szafy sweter (7 możliwości) niebieski 1 (n 1 ) n 2 B n 1 C n 1 N 1 n 1 N 2
biały 2 (b 2 )
zB
zC
zielony (z)
zN 1
zN 2
n 1 B
n 2 C
niebieski 2 (n 2 )
n 2 N 2
n 2 N 1
niebieski 3 (n 3 )
cC
cB
czarny (c) n 3 B n 3 C n 3 N 1 n 3 N 2
cN 1
cN 2
N = 7 · 4 = 28 Stosujemy regułę mnożenia. Karolina może wyciągnąć z szafy 28 różnych
zestawów złożonych ze swetra i spodni.
a) Sweter i spodnie będą w jednym kolorze:

• obie części ubrania mogą być białe – są takie dwie możliwości (b B, b B),
2
1
• obie części ubrania mogą być czarne – jest jedna możliwość (cC),
• obie części ubrania mogą być niebieskie – jest sześć możliwości (n N , n N , n N , n N , n N , n N ).
1
2
2
2
2
3
2
3
1
1
1
1
k = 2 + 1 + 6 = 9 Stosujemy regułę dodawania.
9
P = 28 Obliczamy prawdopodobieństwo.
9
Prawdopodobieństwo, że wyjęte z szafy sweter i spodnie będą w tym samym kolorze, jest równe 28 .
b) Karolina mogła wybrać jeden z 4 swetrów i do każdego swetra dobrać jedną z 4 par spodni.
k = 4 · 4 = 16 Stosujemy regułę mnożenia.
4
P = 16 = Obliczamy prawdopodobieństwo.
28 7
4
Prawdopodobieństwo, że wyjęty z szafy sweter będzie w kolorze zielonym lub niebieskim, jest równe .
7
133