Page 136 - kl 8 cz 2

1. Wśród grupy sportowców, w której jest 9 kobiet (cztery łyżwiarki,
trzy kajakarki, dwie lekkoatletki) i 10 mężczyzn (czterech skoczków
narciarskich, trzech łyżwiarzy, dwóch kajakarzy i jeden wioślarz) należy
wybrać w sposób losowy dwuosobową delegację złożoną z jednej
kobiety i jednego mężczyzny. Oblicz prawdopodobieństwo tego, że:

a) wybrana kobieta uprawia lekkoatletykę i wybrany mężczyzna
uprawia sport wodny,
b) wybrane osoby uprawiają tę samą dyscyplinę sportową.

Przykład 3

Na ściankach czworościennej kostki do gry zapisane są liczby: 20, 21, 22, 23. Rzucamy dwukrotnie tą kostką.
Obliczmy prawdopodobieństwo tego, że:

a) za pierwszym razem zostanie wyrzucona liczba parzysta, a za drugim razem liczba większa od 20,
b) obie wyrzucone liczby będą liczbami pierwszymi lub obie będą liczbami złożonymi,
c) suma wyrzuconych liczb będzie liczbą podzielną przez 5.

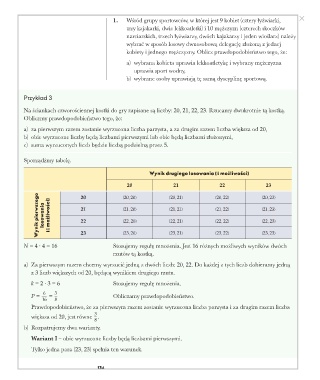
Sporządźmy tabelę.

Wynik drugiego losowania (4 możliwości)
22
23
21
20 (20, 21) (20, 22) (20, 23)
Wynik pierwszego losowania (4 możliwości) 21 (21, 20) (22, 21) (21, 22) (21, 23)
20
(20, 20)
(21, 21)
22
(22, 20)
(22, 23)
(22, 22)
(23, 21)
(23, 22)
(23, 23)
(23, 20)
N = 4 · 4 = 16 23 Stosujemy regułę mnożenia. Jest 16 różnych możliwych wyników dwóch
rzutów tą kostką.
a) Za pierwszym razem chcemy wyrzucić jedną z dwóch liczb: 20, 22. Do każdej z tych liczb dobieramy jedną
z 3 liczb większych od 20, będącą wynikiem drugiego rzutu.
k = 2 · 3 = 6 Stosujemy regułę mnożenia.

6
3
P = 16 = Obliczamy prawdopodobieństwo.
8
Prawdopodobieństwo, że za pierwszym razem zostanie wyrzucona liczba parzysta i za drugim razem liczba
3
większa od 20, jest równe .
8
b) Rozpatrujemy dwa warianty.

Wariant I – obie wyrzucone liczby będą liczbami pierwszymi.
Tylko jedna para (23, 23) spełnia ten warunek.

134